Introduction

Retour à la page du cours

Cette section vous présentera les concepts de base de l'algorithmique, à savoir ce qu'est un algorithme et de quoi il est composé. Vous verrez aussi le cycle de développement, processus par lequel on produit un algorithme et un exemple de problème concret vous sera proposé pour vous le démontrer.

1.1 - Tout d'abord, quelques définitions

1.2 - Le cycle de développement

1.3 - Un premier exemple

1.4 - La compilation

1.1 - Tout d'abord, quelques définitions...

 

Le développement:

Le développement consiste en l'activité de création qui nous permet d'obtenir un programme, une application ou un logiciel.  Ce programme, application ou logiciel est créé dans le but d'apporter une solution à un problème quelconque.

 

La programmation:

La programmation est la partie du développement qui consiste à rédiger du code, dans un langage informatique quelconque, afin d'obtenir ultimement une application.  La rédaction de ce code doit normalement être une traduction d'un algorithme en langage humain vers un langage informatique respectant une syntaxe bien précise.

 

Une application:

Une application est une solution informatique à un problème tiré du monde réel (n'en concluez pas que l'informatique n'est pas réelle pour autant!).  On peut décrire toute application comme un processus qui reçoit de l'information (des données), qui les traite (les transforme ou agit selon elles) et qui nous redonne ensuite d'autres informations.  Ultimement, c'est ce que fait toute application.  Certaines applications le font de façon évidente (par exemple une calculatrice, un fureteur Internet ou un chiffrier électronique), d'autres le font de façon plus subtile (un jeu ou un anti-virus). Les données reçues peuvent provenir d'un humain, d'un fichier ou d'une autre application, tout comme les données émises peuvent être envoyées à un humain, dans un fichier ou à une autre application. Synonymes:  logiciel, programme.

 

Les intrants:

Ce sont les données qui entrent dans l'application, les données que le programme lui-même ne possède pas au départ et qui doivent lui être fournies (que ce soit par un humain, une lecture dans un fichier ou le résultat d'un autre programme).

 

Les extrants:

Ce sont les données qui sortent de l'application, le résultat du programme.  Le but du programme est de produire ces données, normalement à partir des intrants.

 

Un algorithme:

Le mot "algorithme" a été créé en l'honneur de Mohammed Ibn Mussa al-Khuwarizmi (825 avant Jésus-Christ), un mathématicien persan.  Si on prononce rapidement "al-Khuwarizmi", et avec beaucoup d'imagination, on peut arriver à entendre le mot "algorithm" (prononcé en anglais).  Voilà de quoi occuper vos longues soirées d'hiver. Un algorithme n'est rien d'autre qu'une séquence ordonnée d'opérations que l'ordinateur devra réaliser pour produire la solution.  Des exemples d'algorithmes dans la vie de tous les jours?  Une recette de Soeur Angèle, les instructions d'assemblage d'un BBQ, l'itinéraire pour se rendre à l'épluchette de blé d'Inde du beau-frère ou les règles et stratégies gagnantes d'un jeu de société...  Tous ces exemples ne sont rien d'autres que des algorithmes pour un humain, des instructions qui doivent être exécutées dans un certain ordre pour arriver à un but (un gâteau des anges, avoir un BBQ fonctionnel devant soi, arriver à temps pour manger du blé d'Inde ou gagner au Monopoly). L'algorithme que l'on produit en informatique dira à l'ordinateur quoi faire pour atteindre la solution, une étape à la fois.  Un algorithme devra satisfaire les trois conditions suivantes:

Retour à la table des matières de la section

1.2 - Le cycle de développement

Le processus permettant d'obtenir une solution informatique à partir d'un problème est souvent appelé "cycle de développement" parce qu'il est effectivement cyclique:  on revient souvent en arrière tout au long du processus pour recommencer une (ou des) étape(s) réalisée(s) précédemment, pour y appliquer un changement ou une correction.  Il est bien rare que le processus soit suivi d'une façon linéaire, du début jusqu'à une fin.  Les programmes sont en évolution constante et nul n'est à l'abri des erreurs. Il ne faut pas toujours voir le retour en arrière comme une perte de temps qui aurait pu être évitée...  Cela fait partie du processus et c'est tout à fait normal.

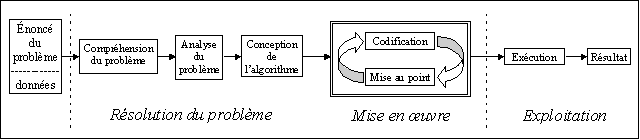
Au départ, le cycle commence par une résolution du problème, de façon théorique, possiblement sans même toucher à l'ordinateur.  Ensuite, l'étape suivante consiste à implanter cette solution théorique sur un ordinateur et à la mettre au point jusqu'à ce qu'elle fonctionne comme prévu.  Finalement, on met l'application obtenue à l'étape précédente en opération et elle est utilisée par des usagers. À chaque étape, il est possible de revenir en arrière:

Phase 1:  la résolution du problème

La phase de résolution du problème consiste à:

Phase 2:  La mise en oeuvre

C'est cette phase qui est aussi appelée "la programmation".  Il s'agit ici simplement de traduire l'algorithme obtenu à la fin de la phase 1 en un langage informatique quelconque.  Ce langage peut être imposé ou choisi en fonction de la solution à implanter.  Dans cette phase, on doit:

Phase 3:  L'exploitation

Durant cette phase, les usagers utiliseront le programme pour obtenir un résultat.  Si le résultat n'est pas satisfaisant ou que les besoins ont changé, on retournera à la phase 1 ou 2 pour recommencer le cycle à partir de là. Même une application qui fonctionne parfaitement n'est jamais réellement terminée...  Les besoins des usagers peuvent (et vont certainement) évoluer et le simple fait d'utiliser l'application générera fort probablement d'autres idées ou d'autres problèmes à résoudre.

Retour à la table des matières de la section

1.3 – Un premier exemple...

Illustrons toutes ces notions avec un exemple tout simple.  Voici le problème:

Phase 1 – Résolution du problème

 

Étape 1.1 – Compréhension du problème

Au départ, il est nécessaire de bien comprendre le problème et d'être certain de cette compréhension.  Si vous avez l'impression que vous n'avez pas tout compris, vous pouvez comparer votre compréhension du problème avec celle qu'en ont vos collègues, ou encore tenter de formuler le problème différemment (ça aide).  Il y a toujours l'option incontournable de poser des questions au client, ici le président de Bouboule-O-Rama. Ce qu'on comprend, c'est que notre application devra pouvoir calculer le volume d'une boule de bowling (l'espace occupé par une sphère), qui pourra être de différente taille d'une exécution à l'autre (de dimension variable).

Étape 1.2 – Analyse du problème

Analysons maintenant le problème pour tenter de le résoudre: En fouillant dans un livre de mathématique, vous apprenez (ou redécouvrez) qu'il existe une formule conçue exprès pour calculer le volume d'une sphère.  Voilà qui nous sera utile.  La formule est:

N'oublions pas que notre analyse a pour but de déterminer les intrants, le traitement et les extrants. Si on examine la formule mathématique, on voit que le volume (V) d'une sphère est égal à 4/3 (quatre tiers, ou un et un tiers) multiplié par pi (une constante mathématique égale à environ 3,14159) multiplié par le rayon de la sphère au cube (multiplié par lui-même trois fois).

4/3 est constant, c'est bien évident.  À chaque exécution de votre application, c'est le même 4/3 qui sera utilisé.  Pi est également constant.  Par contre, ce qui peut varier d'une fois à l'autre, c'est le rayon (r) et le volume (V).  Pour pouvoir calculer le volume d'une sphère, on doit en connaître le rayon.  Voilà qui est un parfait intrant:  l'utilisateur de l'application devra nous donner le rayon de la boule de bowling pour laquelle il veut connaître le volume pour que notre programme puisse le calculer.

Qu'en est-il de V maintenant?  V sera potentiellement différent à chaque exécution du programme?  Évidemment, il pourra être différent, puisqu'il changera selon le résultat du calcul, qui lui-même sera différent selon le rayon obtenu. V est-il un autre intrant alors?  Bien sûr que non, puisque si l'utilisateur du programme devait entrer le volume de sa boule de bowling à chaque fois qu'il utilise le programme, il n'aurait aucun besoin de l'utiliser parce qu'il connaîtrait alors déjà la réponse! V est le volume, c'est ce que notre programme doit calculer.  C'est donc un extrant. Nous avons donc identifié les éléments importants du problème (et par conséquent, de sa solution):

Sachant cela, on peut créer un prototype simple de solution informatique afin de vérifier si notre analyse tient la route.  Par exemple:

 

Ce prototype de solution semble satisfaire les conditions données, on peut donc passer à l'élaboration de l'algorithme proprement dit.  Si jamais cela n'avait pas été le cas, il aurait fallu revenir à l'étape précédente (la compréhension du problème) et vérifier si un détail ne nous aurait pas échappé initialement. Pour nous assurer que tout fonctionne bien par la suite, on élaborera dès maintenant un jeu de tests, c'est à dire un ensemble de données fictives pour lesquelles les réponses sont connues.  Le jeu de tests sera utilisé pour valider notre travail une fois le programme obtenu.  

 

Intrant (rayon)	Extrant (volume)
1	4,1888
2	33,5103
3	113,0972
... ?	... ?

Un bon jeu de tests devra tenter de tenir compte de toutes les situations possibles, incluant celles pour lesquelles quelque chose ne va pas.  On ne peut pas prendre pour acquis (dans un bon programme, une fois qu'on a les notions nécessaires) que l'usager ne va entrer que des intrants jugés "corrects".  Pouvez-vous compléter le tableau du jeu de tests?

Pour l'instant, nous n'avons toutefois pas les notions nécessaires à la gestion d'erreurs dans nos programmes, nous ne pourrons donc pas réagir correctement à ces cas de tests.  Nous nous contenterons de faire des jeux de tests ne contenant que des cas corrects.

Étape 1.3 – Conception de l'algorithme

Maintenant que l'analyse est terminée, concevons notre algorithme.  On sait qu'un algorithme a trois sections principales:

Ces trois étapes doivent être réalisées dans cet ordre puisque le traitement ne peut pas se faire si on n'a pas les intrants et qu'on ne peut pas afficher d'extrants tant que le traitement ne les a pas calculés... On produira alors l'algorithme, sous forme de pseudo-code, c'est à dire un langage structuré comme un langage informatique mais contenant des mots français clairs et simples:  

 

Étape d'entrée	Lire Rayon
Étape de traitement	Volume <- 4/3 * PI * Rayon ^ 3
Étape de sortie	Écrire Volume

Notre pseudo-code contient donc trois lignes, une pour chaque étape.  Un problème plus complexe pourra bien sûr contenir plus de lignes par étape. On considérera que Lire et Écrire sont des "primitives" en pseudo-code, c'est à dire des opérations élémentaires, simples, qu'on prend pour acquises et qu'on n'a pas besoin d'expliquer ou de diviser en sous-étapes.

Remarquez le symbole "<-" à la deuxième ligne.  Il signifie:  "calcule ce qui est à droite et place le résultat dans la variable qui est à gauche".  On appelle cette opération une "assignation" (on y reviendra). Les symboles "*" et "^" sont des symboles arithmétiques pour représenter, respectivement, la multiplication et l'exponentiation.  Ce sont des symboles standards qui sont souvent utilisés en informatique.  Parmi d'autres standards établis, on note le symbole "/" pour la division et bien entendu "+" et "-" pour l'addition et la soustraction.

Reste un détail:  il faut déclarer quelque part la valeur de PI, que l'ordinateur ne connaîtra pas nécessairement.  On fera normalement la déclaration de constantes en début d'algorithme, question de clarté et de régularité, puisque leurs valeurs ne dépendent pas du traitement. Notre algorithme devient donc:

PI <- 3.14159 
Lire  Rayon        
Volume <- 4/3 * PI * Rayon ^ 3         
Écrire  Volume

 

Voilà donc notre algorithme final.  On peut le tester en utilisant des valeurs de rayon simples comme 1 et 2 pour vérifier s'il est toujours satisfaisant.  Si c'est le cas on peut passer à l'étape suivante.  Mais si vous trouvez qu'il est difficile d'écrire un algorithme correct pour régler le problème, c'est probablement parce que l'analyse n'est pas parfaite.  Il faudra donc revenir en arrière.

 

Phase 2 – Mise en oeuvre

 

Étape 2.1 – Codification

Il s'agit ici de traduire notre algorithme en un langage informatique de notre choix.  Nous utiliserons le langage C dans le cadre de ce cours. Normalement, si la phase 1 a été bien faite, l'étape de codification devrait être courte et simple (une fois bien entendu qu'on connaît le langage). On verra cette étape du projet en grands détails dans les prochains cours.

Étape 2.2 – Mise au point

Maintenant que notre programme est créé, reste à le tester pour s'assurer qu'il fonctionne comme prévu.  Pour cela, on applique le jeu de tests et on s'assure qu'on obtient bien les résultats prévus.  Si ce n'est pas le cas, on devra revenir en arrière, d'abord à la codification pour s'assurer que l'on n'a pas fait d'erreurs en traduisant notre pseudo-code en C#. Si la traduction est bonne mais que le programme ne donne toujours pas les bons résultats, c'est signe qu'il faut revenir encore un peu plus loin en arrière pour refaire notre algorithme en pseudo-code:  un détail nous aura échappé...

 

Phase 3 – Exploitation

Dans la phase d'exploitation, c'est l'usager qui travaille.  On lui donne notre application complétée et c'est à lui de l'utiliser.  Toutefois, il est possible qu'il rencontre des problèmes:

Conclusion

Le cycle de développement est un processus dynamique, pendant lequel on fait fréquemment des retours en arrière.  Peu importe notre méthode de travail, c'est inévitable.  Toutefois, il est à notre avantage de détecter les erreurs tôt dans le processus et de s'assurer que chaque étape est complète et réussie avant de passer à la suivante. Pour des problèmes très simples comme celui de l'exemple précédent, toutes ces étapes peuvent sembler superflues et on pourrait croire qu'elles alourdissent inutilement le processus.  En effet, un bon programmeur pourrait très bien discuter avec le client puis passer directement à l'étape de codification.  Toutefois, il faut se rappeler que dans la vie de tous les jours, les problèmes rencontrés pour lesquels on voudra une solution informatique seront bien rarement aussi simplistes que celui de Bouboule-O-Rama! Tenter de gagner du temps en sautant des étapes mène très souvent à une perte de temps encore plus grande plus tard lorsque le problème a une certaine complexité.  C'est pourquoi il est bon de prendre dès maintenant des bonnes habitudes.

Retour à la table des matières de la section

1.4 –  La compilation

Lorsque l'on écrit un programme, on utilise normalement ce qu'on appelle un IDE (Integrated Development Environment – Environnement de développement intégré).  Dans le cadre de ce cours nous utiliserons Visual Studio 2013.  Un IDE nous permet d'éditer notre code (un peu comme dans un traitement de texte) puis de le compiler.  Compiler un programme transforme nos instructions textes en un langage machine compris par le processeur (Ce n'est pas tout à fait vrai dans le monde .NET mais ça revient à peu près au même...). 

Le format résultat est un fichier binaire (donc illisible pour nous) et exécutable (donc lisible par l'ordinateur).  La compilation permet donc de transformer notre code en un fichier compréhensible par l'ordinateur.  Ce fichier pourra être chargé en mémoire puis exécuté. Visual Studio comprend un compilateur qui peut faire ce travail pour nous.  En plus, lorsque ce compilateur n'arrive pas à faire la conversion parce qu'il ne comprend pas notre code, il est normalement facile de trouver nos erreurs et de les corriger grâce aux indices donnés par Visual Studio. Finalement, Visual Studio nous aide tout au long de la rédaction du code en le formatant pour nous, en changeant la couleur des termes qu'il reconnaît et en nous proposant des choix valides lorsque c'est approprié.

Retour à la table des matières de la section

 

Etienne Forest, modifié par Rachid Kadouche 6 septembre, 2016